Théorème de l'axe séparateur (2D)

Tutoriel présenté par : Tankerpat
Date d'écriture : 16 août 2014
Dernière mise à jour : 8 novembre 2015

   Pour gérer les collisions en programmation il y a plusieurs procédés, vous en connaissez sûrement un grand nombre, voir tous, mais la façon de les mettre en place reste assez obscure pour certains. 

   Bon nombre de tutoriels ou de sites partent sur la base que nous sommes des professionnels en maths et en physique si on se met à la programmation. 

   Il nous est alors, difficile de comprendre la base même de certaines équations et de leur utilité. 

   Ce tutoriel est le fruit d'un amateur en programmation, maths et physique, et l'idée et l'envie de le faire sont venues du fait que nous devons souvent réinventer la roue pour pouvoir avancer dans notre jeu afin de le faire évoluer pour soi, pour le rendre plus attractif... 

   Certes, si vous débutez seulement et que vous êtes arrivé ici, sur le site du Meruvia Game Studio, vous vous apercevrez que pour commencer un jeu vous n'êtes plus obligé de réinventer la roue. 

   Jay nous a préparé des tutoriels d'exception très complets et très bien expliqués pour créer son propre jeu, mais en revanche vous devez comprendre son mode de fonctionnement avant d'aller plus loin. 

   C'est d'ailleurs grâce à lui que j'ai continué la programmation en autodidacte (du coup un peu moins ), et donc que j'en suis arrivé là. 

   Les tutoriels complets de Jay sont en C et utilisent la SDL, mais en C# avec XNA, comme on peut le voir dans les news du site, Gondulzak donne un sérieux coup de main à Jay et de ce fait, les tutoriels sur XNA avancent relativement vite (Note de Jay : à l'heure où je mets à jour ce tuto, le Big Tuto XNA 4 de Gondulzak est même terminé ).

   Je vous dis cela car dans ce tutoriel j'utiliserais le langage C# avec XNA et que si vous avez commencé votre jeu en C avec la SDL, la question qui vient de suite : Comment faire pour retranscrire ce tutoriel en C ? 

   Et bien avec la bonne équipe Jay - Gondulzak et un peu de sueur de votre part bien sûr, cela ne devrait pas être trop compliqué. Je m'y attellerais bien mais cela fait un petit moment que je n'ai pas touché à la SDL. 

   Pour ma part, je dirais que la meilleure façon de gérer les collisions tout en restant assez simple, c'est la méthode du SAT (Separating Axis Theorem) qui permet de gérer n'importe quelle collision et d’implémenter la physique comme bon nous semble du moment que les polygones sont convexes.

   Je la trouve assez simple à mettre en place, à condition d'avoir quelques bases en maths et en physique tout de même. 

Téléchargez ce cours en pdf ci-dessous :

   Avant de commencer, nous allons faire quelques petits rappels de mathématiques que nous allons utiliser, mais nous ne traînerons pas non plus ! 

   1- Petits rappels de cours de maths

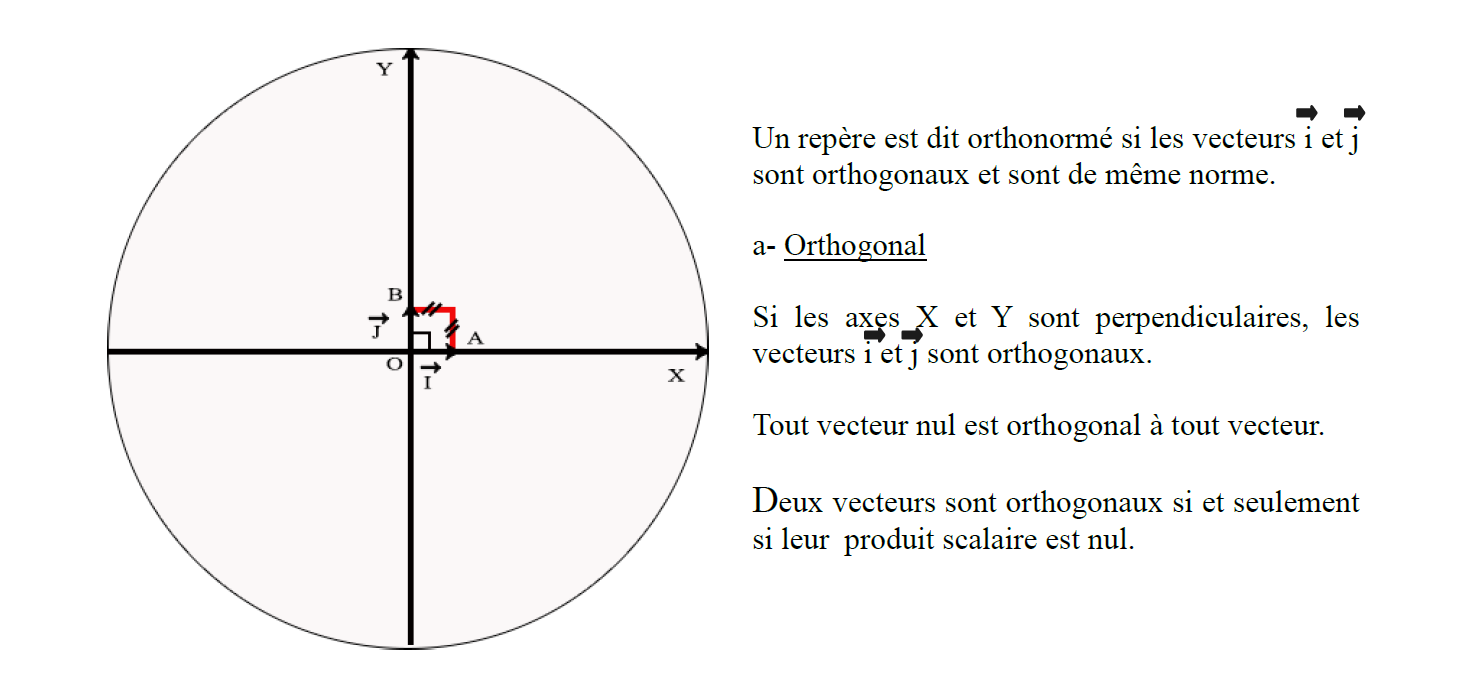
        1.a- Repère orthonormé

        1.b- Norme

        1.c- Normaliser

   Normaliser un vecteur revient à rendre la norme de celui-ci à un.

   Pour normaliser un vecteur il nous faut donc le diviser par sa norme.

        1.d- Normale

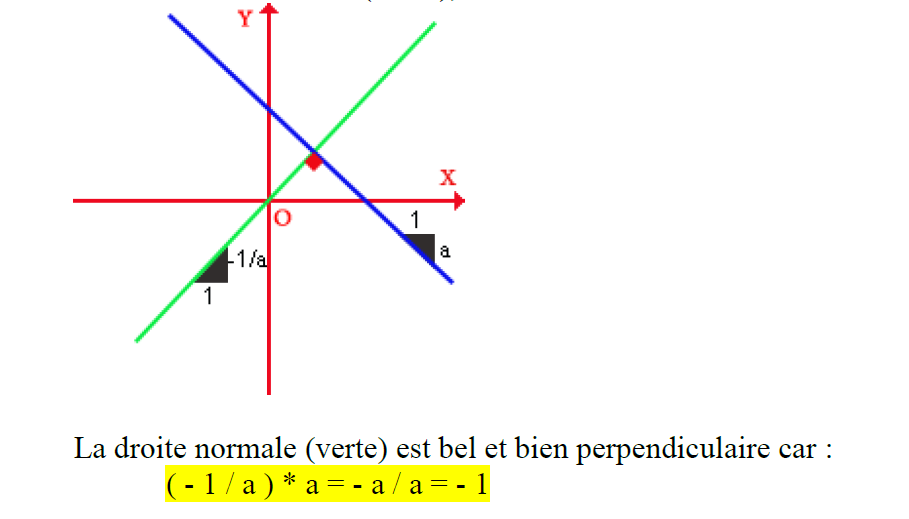
   La droite normale à un plan en un point est la droite orthogonale au plan tangent en ce point. Les droites sont perpendiculaires si et seulement si le produit de leurs coefficients directeurs est égal à -1.

Exemple avec une droite :

   Nous avons une droite (bleue), avec un coefficient directeur de a :

       1.e- Produit vectoriel

        1.f- Produit scalaire

   Bien que son nom lui donne une allure de requin n'ayez pas peur,  il s'apprivoise assez facilement. 

   C’est un outil très utile qui nous servira à calculer la norme d’un vecteur, la projection d’un point sur un axe… 

   2- Les objets

   Comme dit plus haut, la méthode du SAT ne peut être effectuée que si les polygones sont convexes, à l'inverse on dit qu'ils sont concaves.

        2.a- AABB

   Les AABB (Aligned Axis Bounding Box), ce sont les polygones que vous voyez ci-dessus.

   Et oui, effectivement les 4 images sont des AABB (volumes englobants) car leurs axes sont alignés avec le repère orthonormé. Les formes à l'intérieur...  c'est une autre histoire, celle de la collision et de sa réponse. 

        2.b- Cercle : standby

   Les cercles sont à part mais je vous rassure plus simple qu’on ne le pense. 

        2.c- OBB : standby

   Les OBB (Oriented Bounding Box) sont des volumes englobants qui prennent en compte la rotation.

    3- Principe du SAT

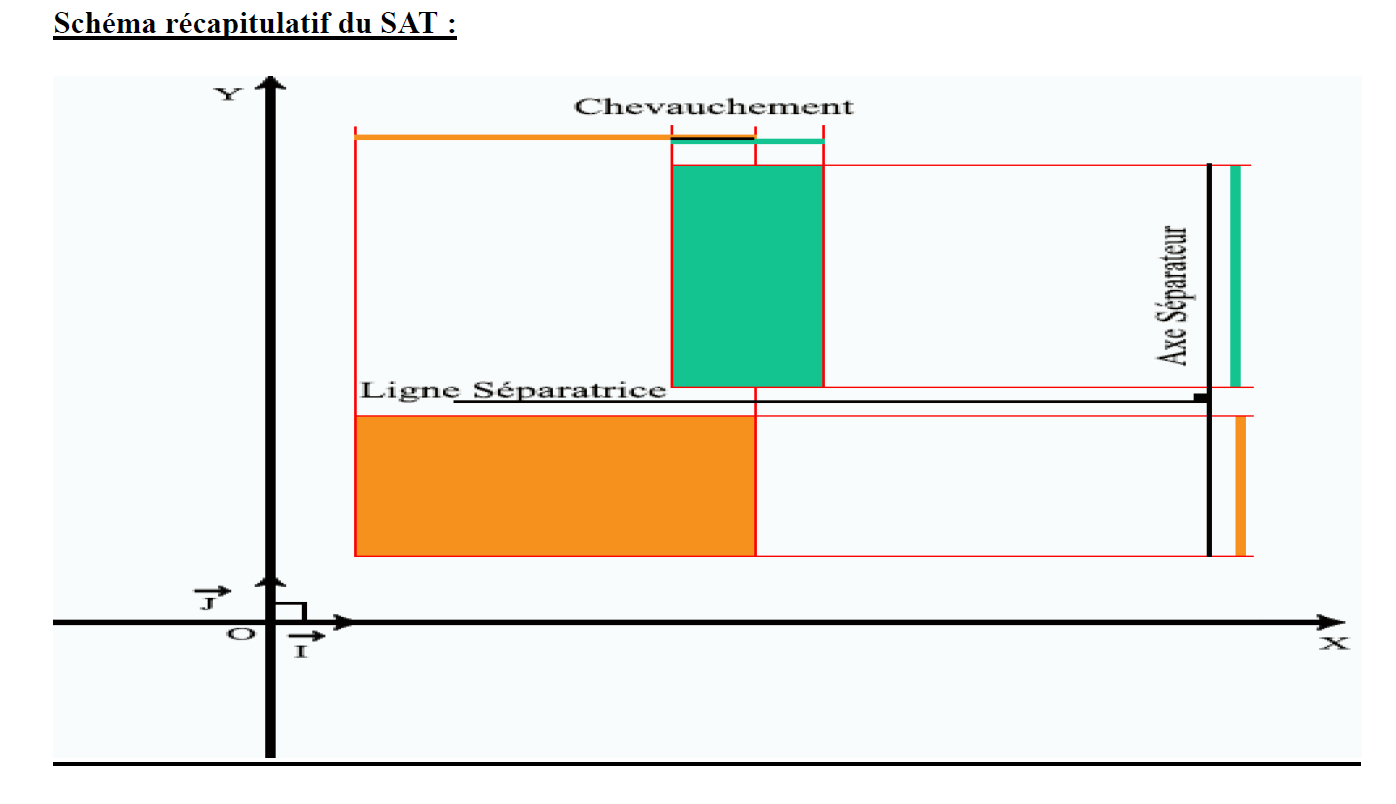
   Le théorème de l’axe séparateur se base sur un principe très simple, s’il y a chevauchement entre toutes les projections (donc il n'y a pas d'axe séparateur) alors il y a collision.

        3.a- AABB

   Nous allons étudier le cas qui nous importe le plus en premier lieu, la tile carré pour les murs/sols, ensuite nous verrons les variantes possibles que l'on peut faire avec la même détection...

   Ci-dessous vous trouverez 2 schémas :

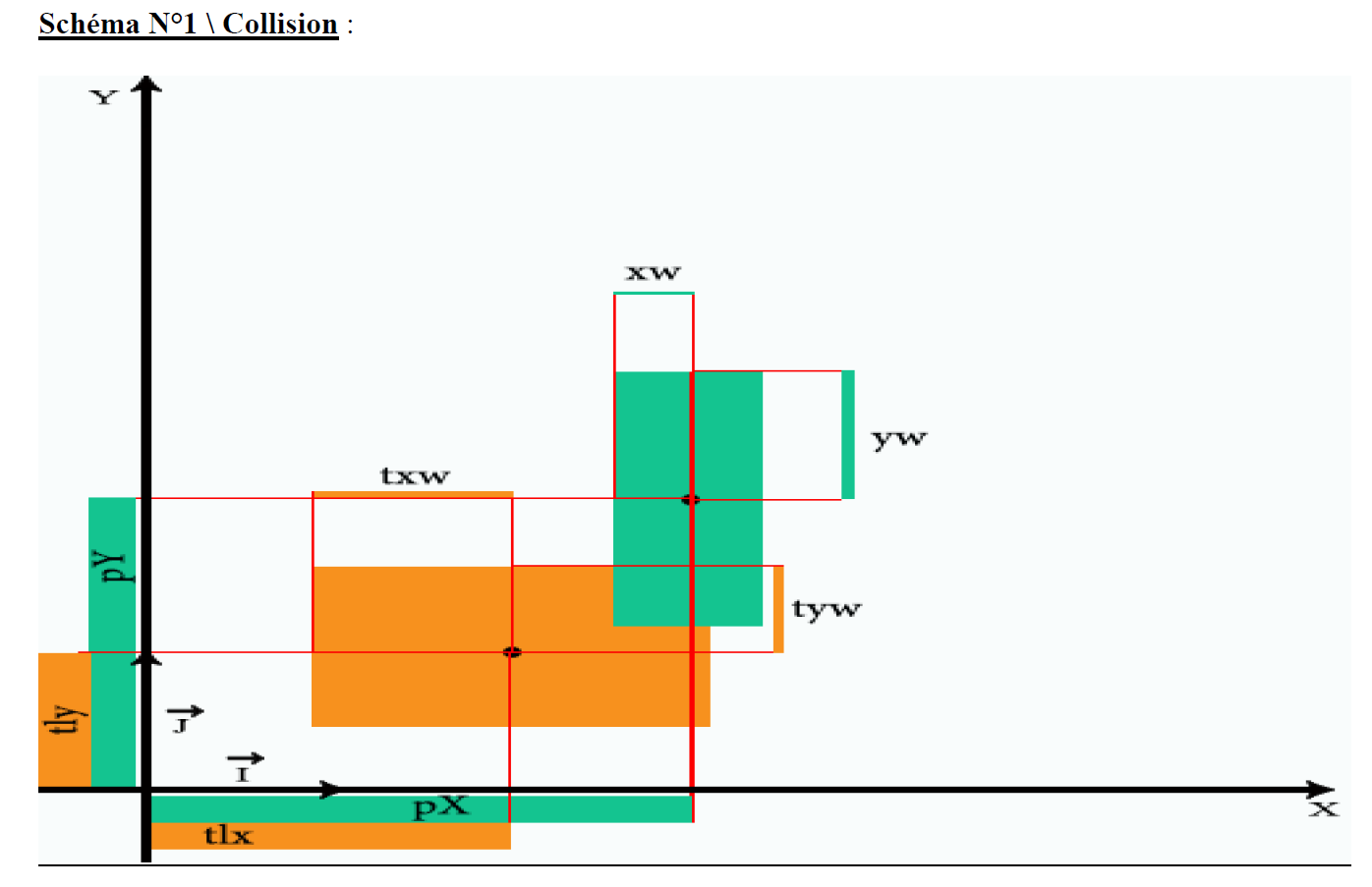
- N°1 - Collision

- N°2 - Pas de collision

        3.b- Mise en pratique

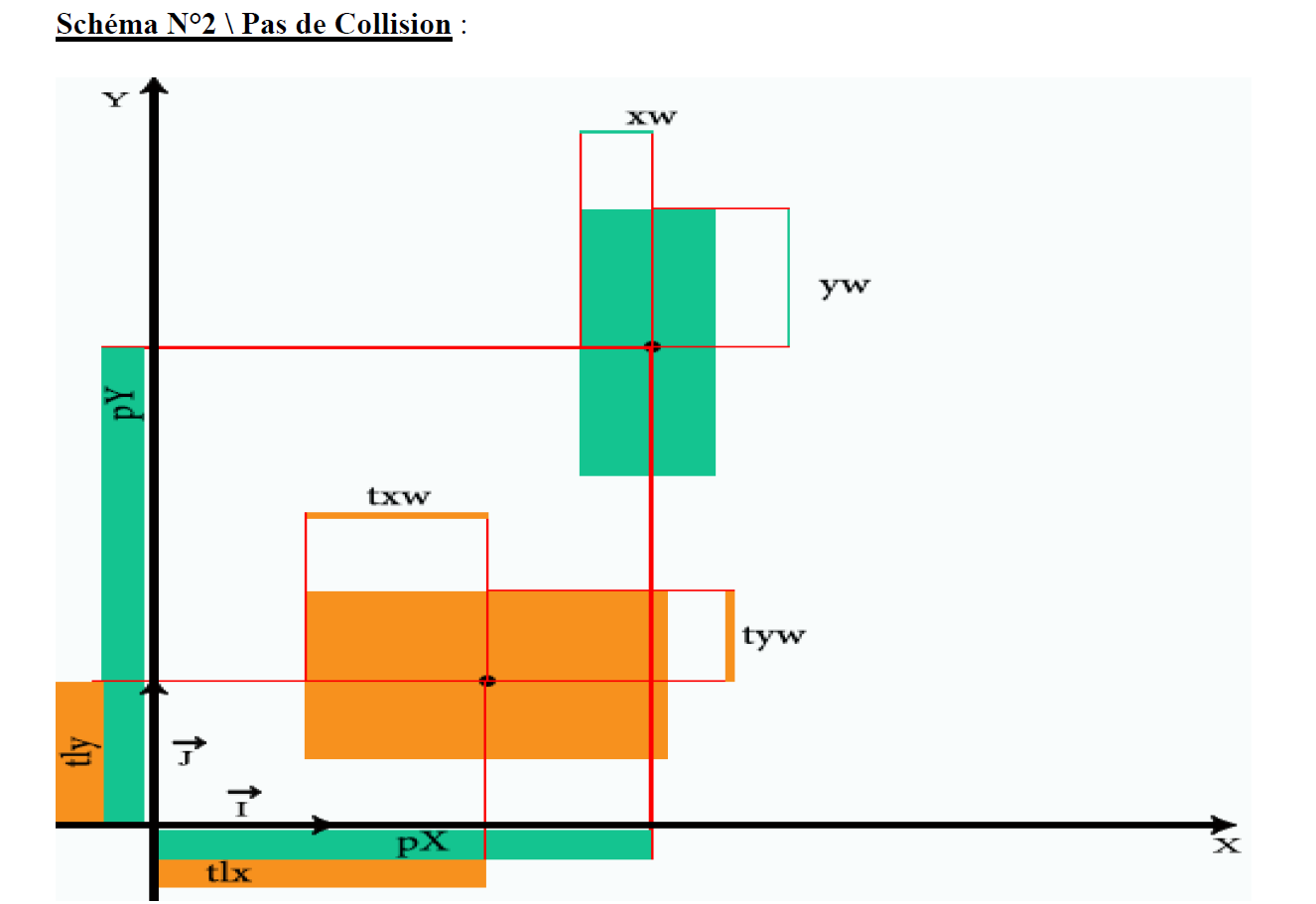
   Commençons par écrire notre petite logique au brouillon.

   Du théorème de l’axe séparateur, nous savons qu’il ne peut y avoir intersection que s’il n’existe pas d’axe séparateur entre la projection de tous les axes.

   A l’inverse, lorsqu’une intersection est détectée, il y a chevauchement sur tous les axes, donc une pénétration en résulte.

   Et commençons par l’axe X.

   Si la pénétration sur l’axe X, que l’on va nommer pénétrationX, est supérieure à 0, alors on continue

   Cela veut donc dire que nous que nous avons un chevauchement sur l’axe X.

   Sinon on quitte.

   Si la pénétration sur l’axe Y, que l’on va nommer pénétrationY, est supérieure à 0, alors on continue.

   Cela veut donc dire que nous que nous avons un chevauchement sur l’axe Y.

   Sinon on quitte.

   Et voilà, nous avons détecté une collision.

   Vous êtes en droit de vous demander « Oui, mais…  Sur quel axe du coup ?  Vu que j’ai une pénétration sur chaque axe ?  ».

   On prendra l’axe qui obtient la plus petite pénétration pour axe de collision. 

   Si vous ne voyez pas, regardez sur le schéma N°1\Collision, et faîtes-vous des mises en scènes.

   Il ne nous reste plus qu’à poser les équations de la détection.

   Notre pénétration n’est ni plus ni moins que notre chevauchement, je vous le rappelle.

   public void RésolutionTile() {}

- si c’est négatif :

o vous comprendrez aisément que l’on multiplie par -1 notre pénétrationX et ce car la projection se fera sur la gauche.

o nous mettons à zéro pénétrationY,

- sinon sur la droite

o nous mettons à zéro pénétrationY.

   Sinon on fait pareil avec la pénétration sur l’axe Y.

   Maintenant il nous faut normer les vecteurs de pénétration afin de normaliser ceux-ci, ce qui va nous permettre d’utiliser les résultats pour pouvoir les intégrer à notre logique physique. 

        3.c- A vous de jouer

   Plus haut, je vous ai dit qu’avec la même détection il nous était possible de gérer plusieurs types de tiles, notamment les pentes… 

   A l’aide du schéma ci-dessous, retrouvez dans un premier temps le signe de la pente de chaque triangle (1ou -1).

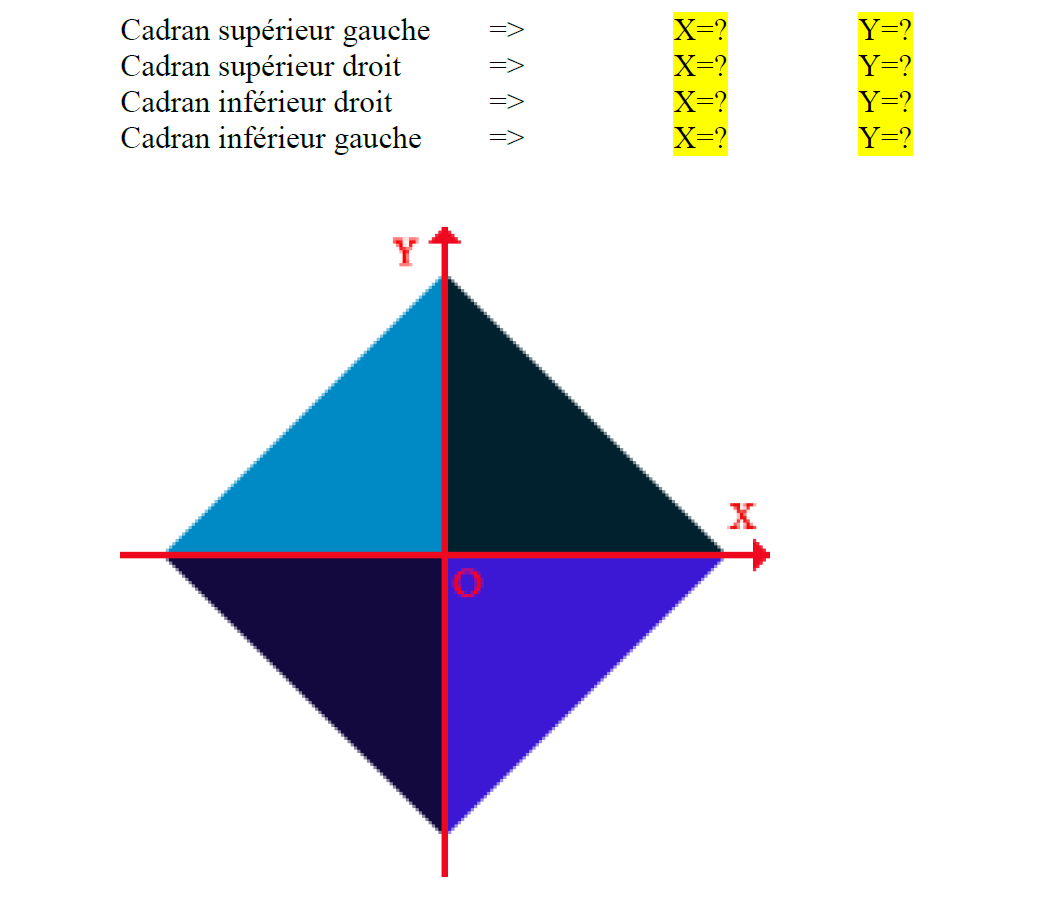
   Il vous faut désormais calculer la distance entre le centre de la tile et le point le plus proche du player.

   Maintenant vous avez toutes les cartes en main afin de réussir. 

   Ne vous inquiétez pas, si vous avez des soucis posez vos questions sur le forum. 

                                                                                                                            Tankerpat.